Тиждень 20
Як зростає чисельність живих істот?
20.1 Дві задачі: про курок і про амеб
20.2 Дивна сила розмноження
20.3 Необмежене розмноження буде зупинене голодом
20.4 Уважні читачі книги Мальтуса
20.5 Природний добір — причина пристосованості
20.6 Про що свідчить історія, яку ми розповіли?
20.7 Перегони між арифметичним та геометричним зростанням
20.8 Як збільшується кількість людей?
Головні думки
● Геометричне зростання (де кожне наступне значення множиться на якесь число, більше за 1), рано чи пізно обганяє будь-яке арифметичне (де до кожного наступного значення додається якесь число).
● Під час розмноження живих істот їх чисельність зростає геометрично. Наслідком є те, що необмежене зростання представників будь-якого виду, від амеб до людей, призведе до вичерпання їжі та необхідного для життя середовища.
● Ті організми, що виживають і розмножуються, частіше краще відповідають своєму способу життя та середовищу, тобто є більш пристосованими.
● Переважне виживання та розмноження більш пристосованих особин називають природним добором.
Опануйте поняття
● Арифметичне зростання
● Геометричне зростання
● Пристосованість
● Природний добір
На цьому тижні йтиметься про математику. Але ж ми вивчаємо природничі науки? Не дивуйтеся цьому. Природничі науки та математика міцно пов’язані. Часто досягнення математики були пов’язані з розв’язуванням нагальних проблем природничих наук. Розквіт природничих наук став наслідком використання математики.
І саме тому ми почнемо з двох простих математичних задач, що наведені у підписах до рисунків. Нічому не дивуйтеся: звісно, умови цих задач є жартівливими!
Задача про курок.
Півтори курки зносять півтора яйця за півтора дня. Скільки яєць знесуть три курки за три дні?
Яка ваша відповідь? Спробуйте порахувати самі, не кваптеся шукати відповідь! Можливо, вам допоможе такий підхід: порахуйте, наскільки збільшилася кількість курок та наскільки збільшився час для відкладання яєць.
Відповіли?
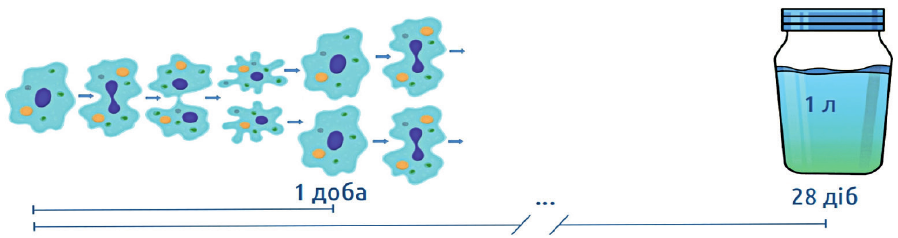
Задача про амеб.
Амеба ділиться навпіл один раз на добу; наступної доби кожен з нащадків також ділиться навпіл. Внаслідок поділу клітин потомство однієї амеби заповнює літрову банку через 28 діб. За який час заповнить літрову банку потомство двох амеб?
Запам’ятайте свою відповідь. Якщо вам важко здогадатися, дайте відповідь на інше питання: за який час потомство однієї амеби заповнить пів банки?
Яка задача здалася вам складнішою — про курок чи про амеб? Насправді складнішою є друга задача, особливо, якщо вирішувати її після першої.
Задача про курок стосується випадку, коли за певний час або за крок розрахунків до попереднього результату додають певне значення. Це — арифметичне зростання. За перші півтора дня буде додано стільки саме яєць, як за наступні.
Задача про амеб стосується випадку, коли за певний час або за крок розрахунків попередній результат множать на якесь число. Це — геометричне зростання. У перший день додається одна амеба, а в останній — пів банки, адже геометричне зростання є таким, що прискорюється.
Тепер ми можемо розповісти вам про значення для історії науки однієї математичної моделі.
Наприкінці XVIII ст. англійський священник Томас Мальтус зробив важливі висновки про те, що розмноження живих істот забезпечує геометричне зростання їх чисельності.

Томас Мальтус (1766–1834). Учений, який довів, що нестримане розмноження будь-яких істот призведе до виснаження їхнього середовища
Розглянемо логіку Мальтуса на тому ж прикладі, з якого ми почали. Дійсно, у найсприятливіших умовах, коли тепло, чисто, та багато їжі, амеба ділиться навпіл один раз на добу. Якщо умови залишаться сприятливими, наступної доби кожна з двох нових особин знову поділиться надвоє. У нашій жартівливій задачі, у разі якщо потомство однієї особини заповнить банку за 28 днів, потомству двох на це залишиться 27 днів. Але чи буває так, щоб помітний простір був зайнятий одними амебами? Звісно, ні. Але якщо б це було можливо, спробуйте вгадати, який об’єм амеби займуть, припустімо, за пів року.
Діаметр амеби, що зіщулилася в кульку — приблизно п’ята частина міліметра. За три з половиною місяці потомки однієї амеби, якби усі вони ділилися як це відбувається у сприятливих умовах, зайняли б об’єм, що дорівнює об’єму Землі. За пів року амеби мали б займати об’єм, що набагато перевищує об’єм Сонячної системи…
Чому ж таке не відбувається? Тому що тільки-но амеб стане багато, вони з’їдять усю їжу, що їх влаштовує, і не залишать вільного простору для свого нормального життя.
Ані амеби, ані будь-які живі істоти не можуть існувати самі по собі. Їм необхідна їжа та відповідне середовище. Після невеликої кількості поділів амебам не вистачить місця для існування та їжі. Вони припинять розмноження або загинуть. І цей висновок стосується не лише амеб, а будь-якого виду живих істот. Звісно, Мальтуса найбільше цікавили люди.
Головний висновок Мальтуса був таким: необмежене розмноження будь-яких істот призведе до вичерпання їжі й усього, що необхідно для їх життя. Мальтус зрозумів, що чисельність людей також може геометрично зростати протягом певного часу. Він вважав, що кількість їжі зростає арифметично, і не цілком мав рацію. Але висновок Мальтуса, що необмежене зростання чисельності людей призведе до перенаселення та голоду, зіграв вагому роль в історії науки.
Книгу Мальтуса прочитало чимало людей; висновки, які вони робили з цієї книги, відповідали рівню їхнього розуміння. Для нас важливо, що в різний час в середині XIX ст. цю книгу прочитали два дослідники природи, що мали багато спільного. Вони, як і Мальтус, були англійцями. Це були зоологи, тобто вчені, які досліджували тваринний світ. Вони подорожували в океані на кораблях і проводили свої дослідження на різних континентах. Обидва бачили відмінності тваринного та рослинного світів різних континентів і різних островів. Обидва шукали причину цих відмінностей. Обидва знайшли рішення після того, як прочитали книгу Мальтуса.
Перший з цих дослідників — Чарльз Дарвін, другий — Альфред Воллес. Обидва зрозуміли, що в природі всі живі істоти не розмножуються з тією швидкістю, на яку здатні. З цього випливає, що переважна кількість особин або не потрапляє у придатні для розмноження умови, або гине до досягнення зрілості.
Цікаво, які саме істоти гинуть, а які лишаються живими та розмножуються?

Чарльз Дарвін (1809–1882) і Альфред Воллес (1823–1913), відкривачі природного добору
Ось воно, рішення! Ті істоти, що відповідають своєму способу життя в умовах свого існування, виживають та розмножуються. Така відповідність має назву пристосованість. Згадайте дзьоби птахів із практичної частини 13 тижня! Ці дзьоби пристосовані кожен для свого способу живлення.
А що відбувається з менш пристосованими організмами, хто гірше відповідає своєму способу життя та своїм умовам? Вони гинуть або залишаються без потомства. Потомство тих, хто вижили та розмножилися, буде різним. Ті з них, хто краще відповідатиме своєму способу життя в умовах, де вони існують, виживуть та розмножаться, а інші — ні…
Першим цю гіпотезу висунув Дарвін. Протягом багатьох років він не оприлюднював її. З часом він отримав листа від Воллеса, який розповів про ту саму здогадку. Дарвін повідомив Воллеса про те, що він раніше дійшов того самого висновку. З часом Дарвін написав книжку, яку скорочено називають «Походження видів». Воллес визнав, що Дарвін був першим, і запропонував називати їх спільні погляди дарвінізмом.
Звісно, з часів Дарвіна та Воллеса наші уявлення щодо причин змін живих організмів з часом стали суттєво детальнішими. Утім, їх головна здогадка блискуче підтвердилася. Причиною змін живих організмів є виживання та розмноження більш пристосованих особин, яке має назву природний добір.
Математики показали, що чисельність живих організмів може зростати геометрично. Це розуміння було дуже простою математичною моделлю розмноження живих істот.
Мальтус зрозумів, що тривале геометричне зростання чисельності будь-якого виду неможливе: його зупинить нестача їжі.
Дарвін та Воллес зрозуміли, що відсторонення від розмноження та загибель організмів залежить від їхньої пристосованості. Переважне виживання та розмноження більш пристосованих організмів називають природним добором. Природний добір, що діяв протягом усієї історії життя на Землі, є причиною пристосованості живих організмів до свого способу життя в характерних для них умовах. Таким чином, математична модель стала важливим кроком у пізнанні причин досконалості живих істот.
Пропонуємо вам просту математичну гру. Порівняймо два ряди чисел. Перший — арифметичне зростання: до кожного значення, починаючи з одиниці, додаватимемо якесь велике число, наприклад, тисячу: 1, 1 001, 2 001, 3 001…
У другому ряді множитимемо кожне значення, починаючи з одиниці, на якесь відносно невелике число, наприклад, на 2: 1, 2, 4, 8…
Який ряд чисел обжене інший: перший чи другий? Перевіримо це розрахунками.
| № у ряді | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Арифметичне зростання |
1 | 1001 | 2001 | 3001 | 4001 | 5001 | 6001 | 7001 | 8001 |
| Геометричне зростання |
1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
| № у ряді | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Арифметичне зростання |
9001 | 10001 | 11001 | 12001 | 13001 | 14001 | 15001 |
| Геометричне зростання |
512 | 1 024 | 2 048 | 4 096 | 8 192 | 16 384 | 32 768 |
Спочатку перший ряд випереджує другий: 3 001 більше, ніж 8. Але якщо ми продовжимо ці ряди, чи збережеться перевага арифметичного зростання? На 15-му кроці геометричне зростання випереджує, а з 16-го кроку можна побачити, що це випередження стає повною «перемогою», і надалі розрив між цими рядами лише зростатиме. Покажемо це на графіку.
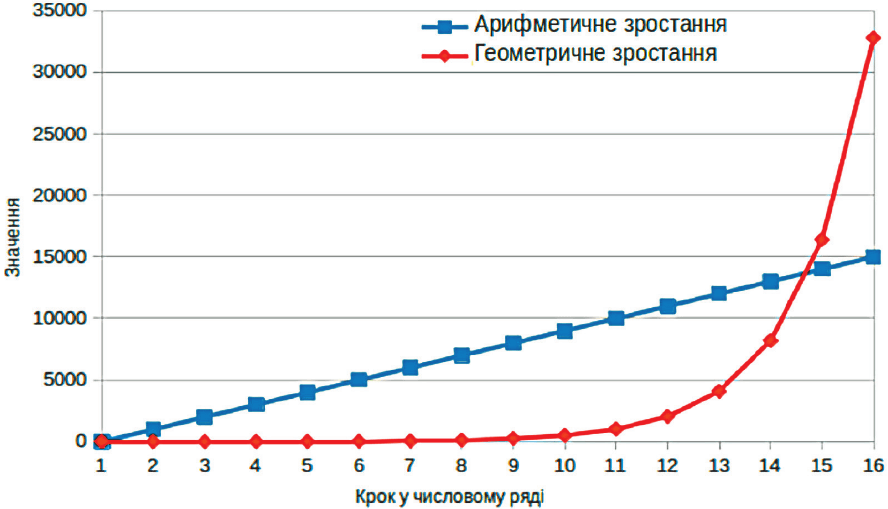
«Змагання» арифметичного та геометричного зростань. До кожного зі значень першого ряду крок за кроком додається певне число. Кожне зі значень другого ряду крок за кроком множиться на певне число
Тепер скажемо ще дивнішу річ. Ряд, у якому до кожного наступного значення додається скільки завгодно велике число, рано чи пізно поступиться ряду, де кожне наступне значення множиться на будь-яке число, вище за одиницю! Так, якщо ми додаватимемо до першого ряду не тисячу, а мільйон, другий ряд обжене його не на 15-му кроці, а на 26-му, але незворотно обжене все одно!
Геометрична прогресія описує не лише зростання чисельності амеб. Зростання чисельності людей також підкоряється такій закономірності. Припустімо, що кожна подружня пара людей до досягнення 25 років народить чотирьох дітей. Кожна пара їх дітей теж буде через 25 років мати четверо дітей. Історія свідчить, що люди можуть розмножуватися з такою швидкістю за сприятливих умов. Через який час за цих умов люди заселять усю Землю?
Припустімо, щоб розмістити одну людину, яка стоїть, потрібна ділянка суходолу 500 × 100 см, пів квадратного метра. Загальна площа суходолу Землі — близько 150 мільйонів км2. Потомство однієї пари людей (за тих фантастичних умов, які ми обговорили) через 1225 років має займати усю площу Землі — з горами, пустелями та льодовиками. Звісно, це настільки ж неможливо, як і те розмноження амеб, яке ми розглядали.
Утім, люди суттєво відрізняються від амеб. У сприятливих умовах швидкість розмноження амеб зростає. У найрозвиненіших країнах, де люди мають усе, що необхідно для їх повноцінного життя, швидкість їх розмноження найчастіше знижується.
В електронній версії підручника використані додаткові завдання, що відрізняються від тих, які містяться у друкованій версії
У стані розробки…


