Головні думки
● Природні явища є закономірними. Ці закономірності можна описувати математично.
● Прикладом вдалого використання математики для опису природних явищ стало відкриття планети Нептун в середині XIX ст.
● Той самий зв’язок між фізичними величинами, можна відобразити різними способами — у вигляді словесного опису, математичної формули, графіка тощо.
Опануйте поняття
● Формула
● Математична модель
● Відношення поверхні до об’єму
● Графік
Імовірно, ви пам’ятаєте, що Земля є третьою планетою Сонячної системи. Ще п’ять планет, від Меркурія до Сатурна, були відомі з давнини, адже їх можна побачити на небі неозброєним оком. Тривалий час здавалося, що далі, ніж Сатурн, планет у Сонячній системі немає.
У XVIII ст. завдяки телескопу (див. 6-й тиждень) було відкрито планету Уран. Відкривач Урану не шукав його спеціально, він просто послідовно досліджував різні ділянки неба. Межі Сонячної системи, що були відомі людству, розсунулися! Астрономи почали вивчати Уран, і, звісно, передусім зацікавилися його рухом по своїй орбіті.
У першій половині XIX ст. вчені навчилися дуже точно розраховувати рух небесних тіл. Закони руху, що були відкриті та втілені в математичні формули Ісааком Ньютоном (ми розповідали про нього на 4-му та 9-му тижні), дозволили розраховувати рух та розташування планет та їхніх супутників.
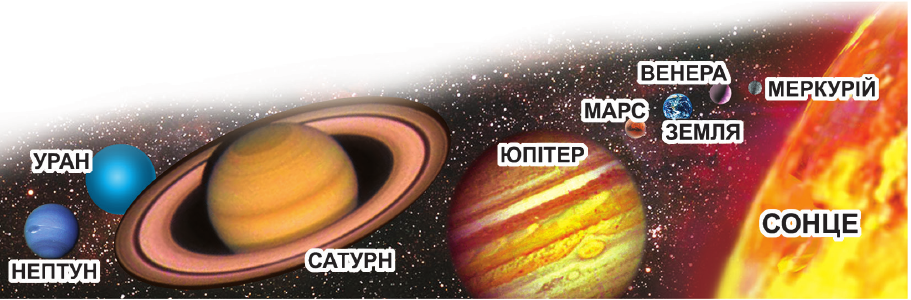
Планети у складі Сонячної системи. Відносні розміри планет збережені, але їх зображення зіставлені поруч
Утім, у русі планети Уран були помічені дивні особливості. Він рухався не так, як мав би за розрахунками вчених. Ви пам’ятаєте, що невідповідність між очікуваннями та спостережуваними фактами є першим кроком у роботі наукового методу? Можливо, на Уран впливає якась нова, невідома на той час планета? Математики почали розрахунки… Першим розв’язав задачу французький математик Урбен Левер’є.
У 1846 році він надіслав свої розрахунки німецькому астроному, який у першу ж ніч спостережень відкрив планету саме там, де її розташування передбачив Левер’є. Цю планету назвали Нептуном. Зараз ми вважаємо, що Нептун — найвіддаленіша від Сонця планета Сонячної системи.

Урбен Левер’є за розрахунками, які дозволили йому передбачити розташування невідомої планети, Нептуну. Коли йдеться про таку величезну роботу, працювати доводиться і вночі…
Фантастичний успіх Левер’є став можливим саме тому, що прояви природи є закономірними, і ці закономірності можна описати математично.
У нашому курсі ми розглядали дві математичні формули, які використовують у фізиці. Перша — це розрахунок швидкості (9-й тиждень):
ν = S : t ,
де ν — швидкість; S — шлях (відстань); t — час руху.
Друга — розрахунок густини (15-й тиждень):
ρ = m : V ,
де ρ — густина; m — маса; V — об’єм.
Що це? Це математичні моделі, що виражені у вигляді формул. Ці моделі символьні. Використовуючи латинські та грецькі букви, ми передаємо зв’язок між фізичними величинами: швидкістю, відстанню та часом або між густиною, масою та об’ємом. Цей зв’язок можна показати по-різному.
Розгляньте графік (графіком називають діаграму, що показує зв’язок між певними величинами). Людина йде зі швидкістю 5 км за годину. Зв’язок між переміщенням людини та часом, за який воно відбувається, показано на графіку червоною лінією. Переконайтеся: відстані 5 км відповідає час, що дорівнює 1 годині! За вдвічі менший час людина пройде вдвічі меншу відстань. А скільки вона пройде за півтори години?
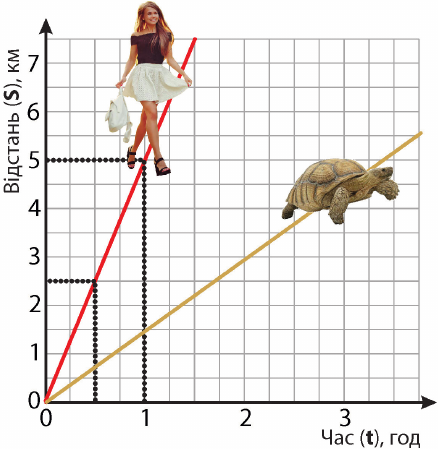
Що показано на цьому графіку? Те саме, що виражено у формулі
ν = S : t.
Лінії на графіку показують, яку відстань і за який час проходять людина та черепаха, які вирушать кожна зі своєю швидкістю
А як відобразити на цьому графіку зв’язок між відстанню та часом переміщення для об’єктів, що вирушать з іншою швидкістю? Їм будуть відповідати інші лінії.
Наступний графік показує густину різних речовин. Що має більшу масу при однаковому об’ємі: каміння (наприклад, граніт), чи залізні речі (наприклад, сталеві, вироблені зі сплаву на основі заліза)? Роздивіться: 1 л (1 кубічний дециметр) граніту важить 2,6 кг, а такий самий об’єм сталі — 7,9 кг, значно більше!
На цьому графіку певну густину показано точкою. Якби ми вказали маси для різних об’ємів кожної з наведених речовин, ці залежності утворили б прямі, як на попередньому графіку.

А на цьому графіку показана густина різних речовин, і відображена залежність
ρ = m : V
На цьому графіку певну густину показано точкою. Якби ми вказали маси для різних об’ємів кожної з наведених речовин, ці залежності утворили б прямі, як на попередньому графіку.
Можливість подати результати наукових досліджень у вигляді формул є сильною стороною науки. Іноді проста формула може зробити цілу наукову революцію.
Так, одним з найбільших досягнень людства є теорія відносності Альберта Ейнштейна (ми згадували його на 4-му тижні). Детальніше ви зрозумієте її пізніше, але дещо розповімо вже зараз. Завдяки дослідженням, які крім іншого, включали роботу з формулами, Ейнштейн зрозумів, що маса та енергія можуть перетворюватися одна на іншу. Формула Ейнштейна E=mc2 (E — енергія, m — маса, c — швидкість світла) відобразила це відкриття. Можливість перетворити масу на енергію, наприклад, використана під час створення атомної бомби.
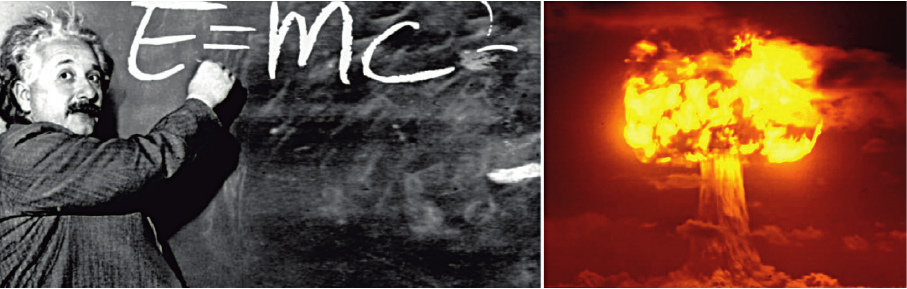
Що є причиною, а що — наслідком? На ілюстрації зображена формула Ейнштейна та її автор (це не справжня фотографія, а колаж — поєднання різних зображень). Ядерний вибух — результат використання нових принципів. До речі, Ейнштейн, праця якого відіграла вагому роль у створенні ядерної зброї, закликав відмовитися від її використання…
Ви знаєте, що фізичні тіла відрізняються не лише за формою, матеріалом та властивостями, а й за розміром.
Цікаво, що змінюється у разі, припустимо, зміни розмірів певного тіла зі збереженням співвідношення між його частинами?
Показані на ілюстрації горняти однакові чи ні? Однакові, якщо не враховувати розмір, але різні за розміром. Чому ці горняти остигають? Гаряча вода віддає своє тепло через поверхню.

Припустіть, у якому з цих горнят окріп вистигне швидше? Чому?
Що більше тепла в окропі, то повільніше остигає горнятко. Що більша поверхня, через яку втрачається тепло, то швидше вистигає горнятко.
Як відрізняється об’єм та площа поверхні у великого та малого горняти? Установимо це на простішому для розрахунків прикладі. Розглянемо два кубики: малий і великий. Припустимо, що довжина їхньої грані відрізняється удвічі.
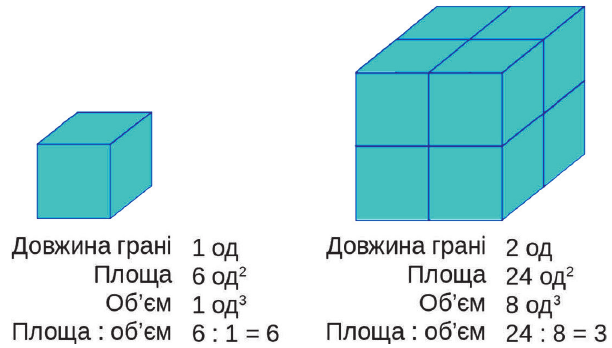
Зі збільшенням розмірів тіла в нього зменшується відношення площі поверхні до об’єму
Яка площа поверхні малого кубика? У нього 6 сторін (3 ми бачимо на рисунку, ще 3 приховані від нас), і в кожної з них площа дорівнює одній квадратній одиниці. Об’єм малого кубика, звісно, — одна кубічна одиниця. Кожна сторона великого кубика має площу 4 квадратні одиниці, усього — 24. Об’єм збільшився у 8 разів. Зрозуміло чому?
Найцікавіше для нас — визначити, як змінилося відношення площі поверхні до об’єму. Як ви бачите, у меншого кубика воно вдвічі більше, ніж у більшого. Те саме можна пояснити навіть без розрахунків. Придивіться: у першому випадку в одиничного кубика всі сторони межують із зовнішнім середовищем, а у другому випадку в кожного такого самого за розміром кубика 3 сторони «дивляться» назовні, а 3 — всередину.
Зі збільшенням розміру тіла відношення площі поверхні до об’єму у нього зменшується. Те ж саме відбувається і з чашками окропу. Менша чашка має більшу відносну поверхню і швидше втрачає тепло.
Ми використовували моделювання під час нашого міркування? Де? Як?
Ми розповіли, як було відкрито планету Нептун. Як не дивно, з часом подібна історія повторилася. Розрахунки руху Нептуна показали, що на нього впливає тяжіння ще якогось небесного тіла. У 1930 р. вдалося відкрити Плутон, який тоді вважали ще однією, дев’ятою планетою Сонячної системи. Він виявився зовсім невеликим. Утім з часом астрономи знайшли кілька об’єктів, що були подібними до Плутона, і вирішили, що він не справжня планета, а карликова.

Карликова планета Плутон у кілька разів менша за Місяць і розташована на холодних і темних околицях Сонячної системи. Плутон так далеко, що Сонце з його поверхні здається лише яскравою зорею…
З Вулканом відбулася ще дивніша історія. Ім’я це планета отримала, але, як виявилося, її не існувало. У середині XIX ст., після того, як Урбен Левер’є знайшов Нептун за відхиленнями орбіти Урана, він узявся за дослідження відхилень орбіти Меркурія, найближчої до Сонця планети. Меркурій також рухається не в повній відповідності до законів Ньютона. Левер’є розрахував, що ці відхилення могла б зумовлювати планета, яку ще до її відкриття назвали Вулканом. Попри тривалі пошуки, знайти цю планету не вдалося. Пояснення особливостей орбіти Меркурія було одержано завдяки теорії відносності, яку запропонував у 1916 р. Альберт Ейнштейн. Річ у тім, що величезне Сонце суттєво викривлює простір поруч із собою, а це зумовлює такі особливості орбіти Меркурія, які неможливо передбачити на підставі законів Ньютона.
В електронній версії підручника використані додаткові завдання, що відрізняються від тих, які містяться у друкованій версії
У стані розробки…


